![]()
Example 4
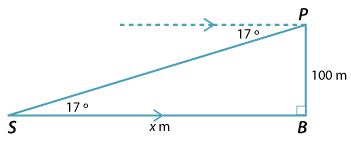
From the top of a cliff, 100 m above sea level, the angle of depression to a ship sailing past is 17°. How far is the ship from the base of the cliff, to the nearest metre?
Solution
With problems like these, always draw a diagram. The diagram shows the top of the cliff \(P\), the ship \(S\) and the base of the cliff \(B\). Let \(SB = x\) m be the distance of the ship from the cliff.
By alternate angles, \(\angle PSB\) = 17°.
Hence
\begin{align}\text{tan} \ 17° \ &= \frac{100}{x} \\ x \ &= \ \frac{100} {\text{tan} \ 17°} \\ &= \ 327.0852\ldots\ \text{m}\end{align}The distance is 327 m (to the nearest metre).